Question:
The balloon, the light rope and the monkey shown in figure are at rest in air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon=M, mass of the monkey $=m$ and length of the rope ascended by the monkey $=L$.
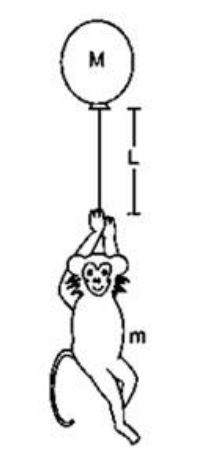
Solution:
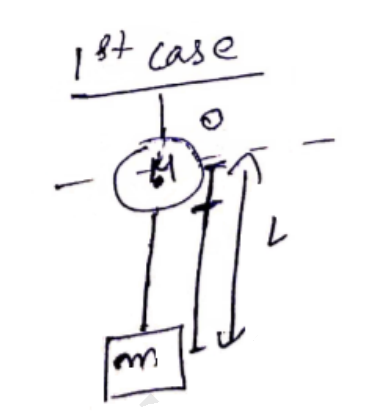
Let balloon be at origin.
$y_{C O M}=\frac{0 . M-L m}{m+M}=0$
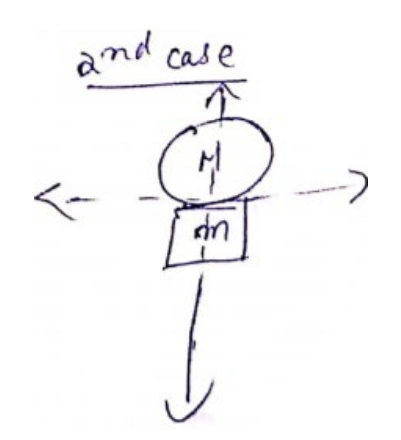
Both monkey and balloon are at origin.
$y_{C O M}^{\circ}=\frac{M(0)+m(0)}{M+m}=0$
Shift= $y_{\text {COM }}^{\prime}-y_{\text {COM }}$
$=\frac{-L m}{M+m}$
So, the balloon descends by $\frac{-L m}{M+m}$ distance.
