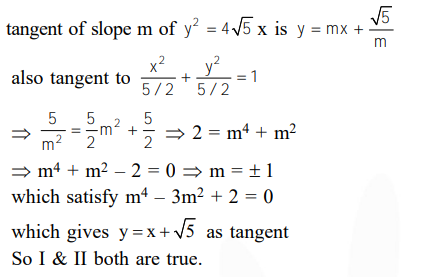Question:
Given : A circle, $2 x^{2}+2 y^{2}=5$ and a parabola, $y^{2}=4 \sqrt{5} x$.
Statement-I : An equation of a common tangent to these curves is $y=x+\sqrt{5}$.
Statement-II : If the line, $\mathrm{y}=\mathrm{mx}+\frac{\sqrt{5}}{\mathrm{~m}}\left(\mathrm{~m}^{1} 0\right)$ is their common tangent, then $\mathrm{m}$ satisfies $\mathrm{m}^{4}$
Correct Option: , 2
Solution: