Question:
Let $\theta_{1}$ be the angle between two lines $2 x+3 y+c_{1}=0$ and $-x+5 y+c_{2}=0$, and $\theta_{2}$ be the angle between two lines $2 x+3 y+c_{1}=0$ and $-x+5 y+c_{3}=0$, where $c_{1}, c_{2}, c_{3}$ are any real numbers :
Statement-1 : If $c_{2}$ and $c_{3}$ are proportional, then $\theta_{1}=\theta_{2}$.
Statement-2 : $\theta_{1}=\theta_{2}$ for all $\mathrm{c}_{2}$ and $\mathrm{c}_{3}$.
Correct Option: , 4
Solution:
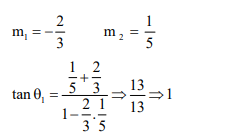
$\tan \theta_{1}=1=\tan \theta_{2}$
$\Rightarrow \theta_{1}=\theta_{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.