Question:
Let $a_{n}$ be the $n^{\text {th }}$ term of an A.P. If $\sum_{r=1}^{100} a_{2 r}=\alpha$ and $\sum_{r=1}^{100} a_{2 r-1}=\beta$, then the common difference of the A.P. is :
Correct Option: , 3
Solution:
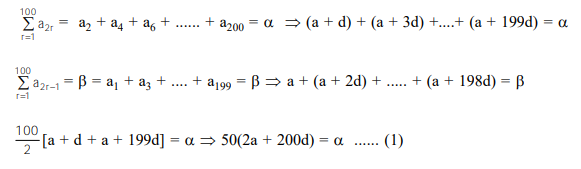
$\frac{100}{2}[\mathrm{a}+\mathrm{a}+198 \mathrm{~d}]=\beta \Rightarrow 50(2 \mathrm{a}+198 \mathrm{~d})=\beta \ldots \ldots(2)$
(1) $-(2) \quad \alpha-\beta=50(2 \mathrm{~d})=\mathrm{d}=\frac{\alpha-\beta}{100}$
