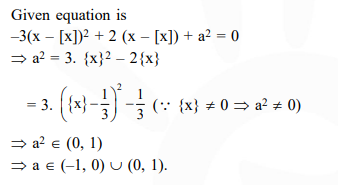Question:
If $\mathrm{a} \in \mathrm{R}$ and the equation $-3(\mathrm{x}-[\mathrm{x}])^{2}+2(\mathrm{x}-[\mathrm{x}])+\mathrm{a}^{2}=0$ (where $[\mathrm{x}]$ deontes the greatest integer $\leq x)$ has no integral solution, then all possible values of a lie in the interval:
Correct Option:
Solution: