Solve each of the following systems of equations by the method of cross-multiplication :

GIVEN: 

$\frac{x}{a}=\frac{y}{b}$

$a x+b y=a^{2}+b^{2}$

To find: The solution of the systems of equation by the method of cross-multiplication:

Here we have the pair of simultaneous equation

$\frac{x}{a}-\frac{y}{b}=0$

$a x+b y-\left(a^{2}+b^{2}\right)=0$

By cross multiplication method we get

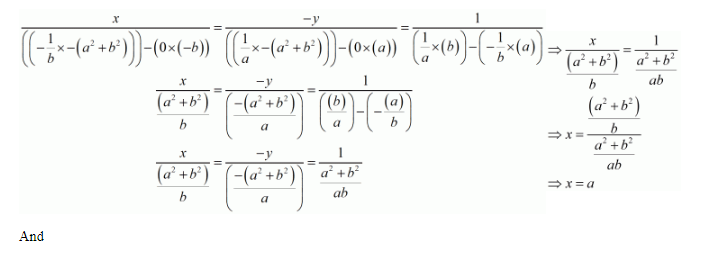
$\frac{-y}{\left(\frac{-\left(a^{2}+b^{2}\right)}{a}\right)}=\frac{1}{\left(\frac{(b)}{a}\right)-\left(-\frac{(a)}{b}\right)}$

$\frac{\frac{-y}{-\left(a^{2}+b^{2}\right)}}{\frac{a}{a}}=\frac{1}{\frac{a^{2}+b^{2}}{a b}}$

$\frac{\frac{y}{\left(a^{2}+b^{2}\right)}}{\frac{a}{a}}=\frac{\frac{1}{a^{2}+b^{2}}}{a b}$

$\Rightarrow y=\frac{\frac{\left(a^{2}+b^{2}\right)}{a}}{\frac{a^{2}+b^{2}}{a b}}$

$\Rightarrow y=b$

Hence we get the value of $x=a$ and $y=b$