Simplify the following using the identities:

(i) Let us consider the following expression:

$\frac{58^{2}-42^{2}}{16}$

Using the identity $(a+b)(a-b)=a^{2}-b^{2}$, we get:

$\frac{58^{2}-42^{2}}{16}=\frac{(58+42)(58-42)}{16}$

$\Rightarrow \frac{58^{2}-42^{2}}{16}=\frac{100 \times 16}{16}$

$\Rightarrow \frac{58^{2}-42^{2}}{16}=100$

Thus, the answer is 100.

(ii) Let us consider the following expression:

$178 \times 178-22 \times 22$

Using the identity $(a+b)(a-b)=a^{2}-b^{2}$, we get:

$178 \times 178-22 \times 22=178^{2}-22^{2}=(178+22)(178-22)=200 \times 156=31200$

Thus, the answer is 31200.

(iii) Let us consider the following expression:

$\frac{198 \times 198-102 \times 102}{96}=\frac{198^{2}-102^{2}}{96}$

Using the identity $(a+b)(a-b)=a^{2}-b^{2}$, we get:

$\frac{198 \times 198-102 \times 102}{96}=\frac{198^{2}-102^{2}}{96}=\frac{(198+102)(198-102)}{96}$

$\Rightarrow \frac{198 \times 198-102 \times 102}{96}=\frac{(198+102)(198-102)}{96}$

$\Rightarrow \frac{198 \times 198-102 \times 102}{96}=\frac{300 \times 96}{96}$

$\Rightarrow \frac{198 \times 198-102 \times 102}{96}=300$

Thus, the answer is 300.

(iv) Let us consider the following expression:

$1.73 \times 1.73-0.27 \times 0.27$

Using the identity $(a+b)(a-b)=a^{2}-b^{2}$, we get:

$1.73 \times 1.73-0.27 \times 0.27=1.73^{2}-0.27^{2}=(1.73+0.27)(1.73-0.27)=2 \times 1.46=2.92$

Thus, the answer is 2.92.

(v) Let us consider the following expression:

$\frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=\frac{8.63^{2}-1.37^{2}}{0.726}$

Using the identity $(a+b)(a-b)=a^{2}-b^{2}$, we get:

$\frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=\frac{8.63^{2}-1.37^{2}}{0.726}=\frac{(8.63+1.37)(8.63-1.37)}{0.726}$

$\Rightarrow \frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=\frac{(8.63+1.37)(8.63-1.37)}{0.726}$

$\Rightarrow \frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=\frac{(8.63+1.37)(8.63-1.37)}{0.726}$

$\Rightarrow \frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=\frac{10 \times 7.26}{0.726}$

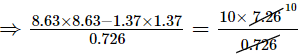
$\Rightarrow \frac{8.63 \times 8.63-1.37 \times 1.37}{0.726}=100$

Thus, the answer is 100.