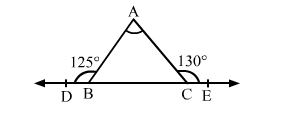
Side BC of ∆ABC has been produced to D on left and to E on right hand side of BC such that ∠ABD = 125° and ∠ACE = 130°.

(d) 75°

We have :

$\therefore \angle A B D+\angle A B C=180^{\circ} \quad[\because D E$ is a straight line $]$

$\Rightarrow 125^{\circ}+\angle A B C=180^{\circ}$

$\Rightarrow \angle A B C=55^{\circ}$

Also,

$\angle A C E+\angle A C B=180^{\circ}$

$\Rightarrow 130^{\circ}+\angle A C B=180^{\circ}$

$\Rightarrow \angle A C B=50^{\circ}$

$\therefore \angle B A C+\angle A B C+\angle A C B=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow \angle B A C+55^{\circ}+50^{\circ}=180^{\circ}$

$\Rightarrow \angle B A C=75^{\circ}$

$\Rightarrow \angle A=75^{\circ}$