Show that the quadrilateral formed by the straight lines

Solving the euations we get the coordinates of the quadrilateral.

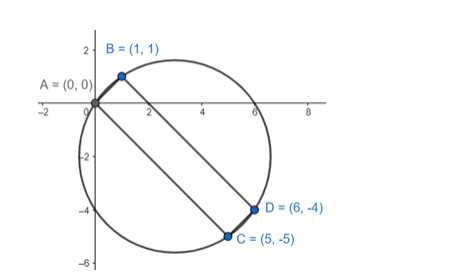
Slope of $\mathrm{AB}=\frac{1-0}{1-0}=1$

Slope of $C D=1$

$\mathrm{AB} \| \mathrm{CD}$

Slope of $B D=A C=-1$

$A C \| B D$

So they form a rectangle with all sides $=90^{\circ}$

The quadrilateral is cyclic as sum of opposite angles $=180^{\circ}$.

Now, $A D=$ diameter of the circle equation of the circle with extremities $A(0,0) \& D(6,-4)$ is

$(x-0)(x-6)+(y-0)(y+4)=0$

$x^{2}+y^{2}-6 x+4 y=0$