Show that the quadrilateral formed

Given In a square $A B C D, P, Q, R$ and $S$ are the mid-points of $A B$, $B C, C D$ and $D A$, respectively.

To show $P Q R S$ is a square.

Construction Join $A C$ and $B D$.

Proof Since, $A B C D$ is a square.

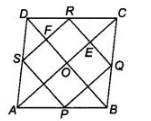
$\therefore \quad A B=B C=C D=A D$

Also, $P, Q, R$ and $S$ are the mid-points of $A B, B C, C D$ and $D A$, respectively.

Then, in $\triangle A D C$, $S R \| A C$ 

and  $S R=\frac{1}{2} A C$ [by mid-point theorem]...(i)

$\ln \triangle A B C$, $P Q \| A C$

and

$P Q=\frac{1}{2} A C$ ... (ii)

From Eqs. (i) and (ii), 

$S R \| P Q$ and $S R=P Q=\frac{1}{2} A C$ ...(iii)

Similarly, $S P \| B D$ and $B D \| R Q$

$\therefore$ $S P \| R Q$ and $S P=\frac{1}{2} B D$

and  $R Q=\frac{1}{2} B D$

$\therefore$ $S P=R Q=\frac{1}{2} B D$

Since, diagonals of a square bisect each other at right angle.

$\therefore \quad A C=B D$

$\Rightarrow \quad S P=R Q=\frac{1}{2} A C$ $\ldots(\mathrm{i} \mathrm{v})$

From Eqs. (iii) and (iv), $\quad S \dot{R}=P Q=S P=R Q$ [all side are equal]

Now, in quadrilateral OERF,

$O E \| F R$ and $O F \| E R$

$\therefore \quad \angle E O F=\angle E R F=90^{\circ}$

Hence, $P Q R S$ is a square.

Hence proved.