Show that the points A

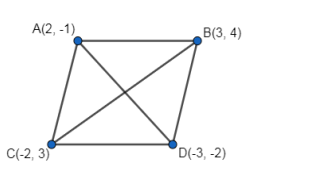
Given: Vertices of the quadrilateral are $\mathrm{A}(2,-1), \mathrm{B}(3,4), \mathrm{C}(-2,3)$ and $\mathrm{D}(-3,-2)$.

Note: For a quadrilateral to be a rhombus, all the sides must be equal in length and the diagonals must not be equal.

$A B=\sqrt{(3-2)^{2}+(4+1)^{2}}=\sqrt{1+25}$

$=\sqrt{26 \text { units }}$

$B C=\sqrt{(-2-3)^{2}+(3-4)^{2}}=\sqrt{25+1}$

$=\sqrt{26}$ units

$C D=\sqrt{(-3+2)^{2}+(-2-3)^{2}}=\sqrt{1+25}$

$=\sqrt{26}$ units

$D A=\sqrt{(2+3)^{2}+(-1+2)^{2}}=\sqrt{25+1}$

$=\sqrt{2} 6$ units

Therefore, $A B=B C=C D=D A \ldots . .(1)$

$A C=\sqrt{(-2-2)^{2}+(3+1)^{2}}=\sqrt{16+16}$

$=4 \sqrt{2}$ units

$B D=\sqrt{(-3-3)^{2}+(-2-4)^{2}}=\sqrt{36+36}$

$=6 \sqrt{2}$ units

Also, $A C \neq B D$ ..............(2)

From 1 and 2, we have all the sides are equal and diagonals are not equal.

Hence, the points A, B, C and D are the vertices of a rhombus.