Show that the points A (1, 2), B (-1, -16) and C (0, -7) lie on the graph of the linear equation y = 9x – 7.
Thinking Process
(i) Firstly, make a table for the equation y = 9x – 7.
(ii) Secondly, plot the obtained points from the table on a graph and join them to get a straight line.
(iii) Further, we plot the given points on a graph paper and find that whether these points lie on the line or not.
Firstly, to draw the graph of equation
$y=9 x-7$
When $x=2$, then $y=9 \times 2-7$
$=18-7=11$
When $x=-2$, then $y=9 \times-2-7$
$=-18-7=-25$
Here, we find two points $D(2,11)$ and $E(-2,-25)$.
So, draw the graph by plotting the points and joining the line $D E$.
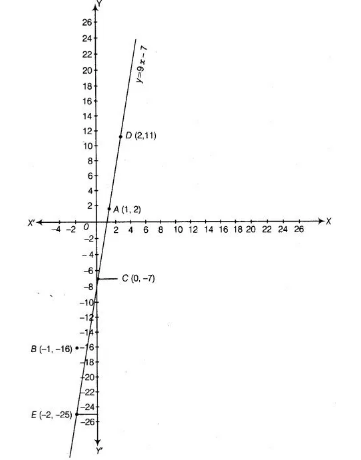
Now, we plot the given points A (1,2), B (-1, -16) and C (0, -7) on the graph paper. We see that all the points lie on DE line.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.