Show that the function

(i) $f: N \rightarrow N: f(x)=x^{3}$ is one - one into.

$f(x)=x^{3}$

Since the function f(x) is monotonically increasing from the domain N → N

$\therefore f(x)$ is one -one

Range of $f(x)=(-\infty, \infty) \neq N$ (codomain)

$\therefore f(x)$ is into

$\therefore f: N \rightarrow N: f(x)=x^{2}$ is one - one into.

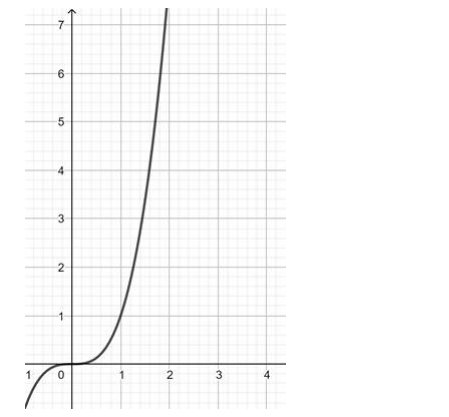
(ii) $f: Z \rightarrow Z: f(x)=x^{3}$ is one - one into

$f(x)=x^{3}$

Since the function $f(x)$ is monotonically increasing from the domain $Z \rightarrow Z$

$\therefore f(x)$ is one -one

Range of $f(x)=(-\infty, \infty) \neq Z$ (codomain)

$\therefore f(x)$ is into

$\therefore f: Z \rightarrow Z: f(x)=x^{3}$ is one - one into.