Show that the diagonals of a square are equal and bisect each other at right angles.

Solution:



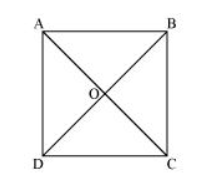
Let $A B C D$ be a square. Let the diagonals $A C$ and $B D$ intersect each other at a point $O$. To prove that the diagonals of a square are equal and bisect each other at right angles, we have to prove $A C=B D, O A=O C, O B=O D$, and $\angle A O B=90^{\circ}$.

In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DCB}$,

$A B=D C$ (Sides of a square are equal to each other)

$\angle A B C=\angle D C B$ (All interior angles are of $90^{\circ}$ )

$\mathrm{BC}=\mathrm{CB}$ (Common side)

$\therefore \triangle \mathrm{ABC} \cong \triangle \mathrm{DCB}$ (By $S \mathrm{AS}$ congruency)

$\therefore \mathrm{AC}=\mathrm{DB}(\mathrm{By} \mathrm{CPCT})$

Hence, the diagonals of a square are equal in length.

In $\triangle \mathrm{AOB}$ and $\triangle \mathrm{COD}$

$\angle A O B=\angle C O D$ (Vertically opposite angles)

$\angle \mathrm{ABO}=\angle \mathrm{CDO}$ (Alternate interior angles)

$A B=C D$ (Sides of a square are always equal)

$\therefore \triangle \mathrm{AOB} \cong \triangle \mathrm{COD}(\mathrm{By} \mathrm{AAS}$ congruence rule)

$\therefore A O=C O$ and $O B=O D(B y C P C T)$

Hence, the diagonals of a square bisect each other.

In $\triangle \mathrm{AOB}$ and $\triangle \mathrm{COB}$

As we had proved that diagonals bisect each other, therefore,

$A O=C O$

$A B=C B$ (Sides of a square are equal)

$\mathrm{BO}=\mathrm{BO}$ (Common)

$\therefore \triangle \mathrm{AOB} \cong \triangle \mathrm{COB}$ (By $S S S$ congruency)

$\therefore \angle A O B=\angle C O B(B y C P C T)$

However, $\angle A O B+\angle C O B=180^{\circ}$ (Linear pair)

$2 \angle \mathrm{AOB}=180^{\circ}$

$\angle \mathrm{AOB}=90^{\circ}$

Hence, the diagonals of a square bisect each other at right angles.