Show that the angles of an equilateral triangle are 60º each.

Solution:



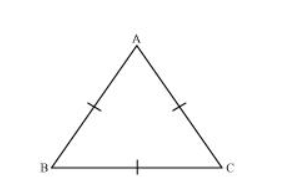
Let us consider that $\mathrm{ABC}$ is an equilateral triangle.

Therefore, $A B=B C=A C$

$A B=A C$

$\Rightarrow \angle C=\angle B$ (Angles opposite to equal sides of a triangle are equal)

Also,

$\mathrm{AC}=\mathrm{BC}$

$\Rightarrow \angle B=\angle A$ (Angles opposite to equal sides of a triangle are equal)

Therefore, we obtain

$\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}$

In $\triangle \mathrm{ABC}$

$\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}$

$\Rightarrow \angle \mathrm{A}+\angle \mathrm{A}+\angle \mathrm{A}=180^{\circ}$

$\Rightarrow 3 \angle \mathrm{A}=180^{\circ}$

$\Rightarrow \angle \mathrm{A}=60^{\circ}$

$\Rightarrow \angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=60^{\circ}$

Hence, in an equilateral triangle, all interior angles are of measure $60^{\circ}$.