Show that in a quadrilateral ABCD, AB + BC + CD + DA< 2 (BD + AC)
Thinking Process
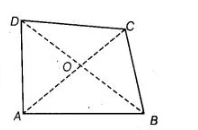
Firstly, draw a quadrilateral ABCD. Further use the property of a triangle that sum of two sides of a triangle is greater than third side and show the
required result.
Given $A B C D$ is a quadrilateral.
To show $\quad A B+B C+C D+D A<2(B D+A C)$
Construction Join diagonals $A C$ and $B D$.
Proof in $\triangle O A B$, $O A+O B>A B$ $\cdots(1)$
[sum of two sides of a triangle is greater than the third side]
In $\triangle O B C, \quad \quad O B+O C>B C$. ... (ii)
[sum of two sides of a triangle is greater than the third side]
In $\triangle O C D, \quad O C+O D>C D$ ...(iii)
[sum of two sides of a triangle is greater than the third side]
In $\triangle O D A$, $O D+O A>D A$ $\ldots($ iv $)$
[sum of two sides of a triangle is greater than the third side]
On adding Eqs. (i), (ii), (iii) and (iv), we get
$2[(O A+O B+O C+O D]>A B+B C+C D+D A$
$\Rightarrow \quad 2[(O A+O C)+(O B+O D)]>A B+B C+C D+D A$
$\Rightarrow \quad 2(A C+B D)>A B+B C+C D+D A$
$[\because O A+O C=A C$ and $O B+O D=B D]$
$\Rightarrow \quad A B+B C+C D+D A<2(B D+A C)$
