Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Solution:



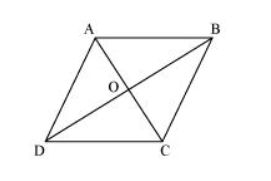
Let $A B C D$ be a quadrilateral, whose diagonals $A C$ and $B D$ bisect each other at right angle i.e., $O A=O C, O B=O D$, and $\angle A O B=\angle B O C=$ $\angle C O D=\angle A O D=90^{\circ} .$ To prove $A B C D$ a rhombus, we have to prove $A B C D$ is a parallelogram and all the sides of $A B C D$ are equal.

In $\triangle \mathrm{AOD}$ and $\triangle C O D$,

$O A=O C$ (Diagonals bisect each other)

$\angle \mathrm{AOD}=\angle \mathrm{COD}$ (Given)

OD = OD (Common)

$\therefore \triangle \mathrm{AOD} \cong \triangle \mathrm{COD}($ By $S A S$ congruence rule $)$

$\therefore A D=C D(1)$

Similarly, it can be proved that

$\mathrm{AD}=\mathrm{AB}$ and $\mathrm{CD}=\mathrm{BC}(2)$

From equations (1) and (2),

$A B=B C=C D=A D$

Since opposite sides of quadrilateral $A B C D$ are equal, it can be said that $A B C D$ is a parallelogram. Since all sides of a parallelogram $A B C D$ are equal, it can be said that $A B C D$ is a rhombus.