Show that f is invertible. Find the inverse of f.

Solution:

$f: \mathbf{R} \rightarrow \mathbf{R}$ is given by,

$f(x)=4 x+3$

One-one:

Let $f(x)=f(y)$

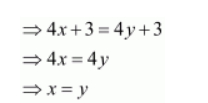
∴ f is a one-one function.

Onto:

For $y \in \mathbf{R}$, let $y=4 x+3$

$\Rightarrow x=\frac{y-3}{4} \in \mathbf{R}$

Therefore, for any $y \in \mathbf{R}$, there exists $x=\frac{y-3}{4} \in \mathbf{R}$ such that

$f(x)=f\left(\frac{y-3}{4}\right)=4\left(\frac{y-3}{4}\right)+3=y$

∴ f is onto.

Thus, $f$ is one-one and onto and therefore, $f^{-1}$ exists.

Let us define $g: \mathbf{R} \rightarrow \mathbf{R}$ by $g(x)=\frac{y-3}{4}$.

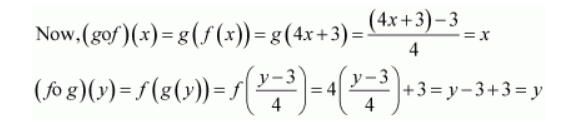
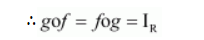
Hence, f is invertible and the inverse of f is given by

$f^{-1}(y)=g(y)=\frac{y-3}{4}$