Question:
Show that a diagonal divides a parallelogram into two triangles of equal area.
Solution:
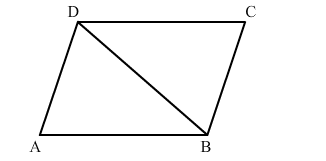
Let ABCD be a parallelogram and BD be its diagonal.
To prove: ar(∆ABD) = ar(∆CDB)
Proof:
In ∆ABD and ∆CDB, we have:
AB = CD [Opposite sides of a parallelogram]
AD = CB [Opposite sides of a parallelogram]
BD = DB [Common]
i.e., ∆ABD ≅ ∆CDB [ SSS criteria]
∴ ar(∆ABD) = ar(∆CDB)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.