Show that A B=B A in each of the following cases:

Given : $A=\left[\begin{array}{ccc}1 & 3 & -1 \\ 2 & 2 & -1 \\ 3 & 0 & -1\end{array}\right]$ and $B=\left[\begin{array}{ccc}-2 & 3 & -1 \\ -1 & 2 & -1 \\ -6 & 9 & -4\end{array}\right]$

Matrix A is of order $3 \times 3$ and Matrix $B$ is of order $3 \times 3$

To show : matrix $\mathrm{AB}=\mathrm{BA}$

If $A$ is a matrix of order $a \times b$ and $B$ is a matrix of order $c \times d$, then matrix $A B$ exists and is of order $a \times d$, if and only if $b=$ C

If $A$ is a matrix of order $a \times b$ and $B$ is a matrix of order $c \times d$, then matrix BA exists and is of order $c \times b$, if and only if $d=$ $a$

For matrix $A B, a=3, b=c=3, d=3$, thus matrix $A B$ is of order $3 \times 3$

Matrix $\mathrm{AB}=\left[\begin{array}{ccc}1 & 3 & -1 \\ 2 & 2 & -1 \\ 3 & 0 & -1\end{array}\right] \times\left[\begin{array}{ccc}-2 & 3 & -1 \\ -1 & 2 & -1 \\ -6 & 9 & -4\end{array}\right]=$

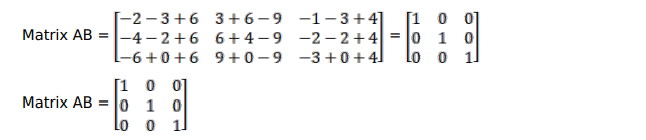
For matrix $B A, a=3, b=c=3, d=3$, thus matrix $A B$ is of order $3 \times 3$

Matrix $B A=\left[\begin{array}{lll}-2 & 3 & -1 \\ -1 & 2 & -1 \\ -6 & 9 & -4\end{array}\right] \times\left[\begin{array}{lll}1 & 3 & -1 \\ 2 & 2 & -1 \\ 3 & 0 & -1\end{array}\right]$

Matrix $B A=\left[\begin{array}{lll}-2(1)+3(2)-1(3) & -2(3)+3(2)-1(0) & -2(-1)+3(-1)-1(-1) \\ -1(1)+2(2)-1(3) & -1(3)+2(2)-1(0) & -1(-1)+2(-1)-1(-1) \\ -6(1)+9(2)-4(3) & -6(3)+9(2)-4(0) & -6(-1)+9(-1)-4(-1)\end{array}\right]$

Matrix BA $=\left[\begin{array}{ccc}-2+6-3 & -6+6+0 & 2-3+1 \\ -1+2-3 & -3+4+0 & 1-2+1 \\ -6+18-12 & -18+18+0 & 6-9+4\end{array}\right]$

Matrix BA $=\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$

Matrix $A B=$ Matrix $B A=\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$