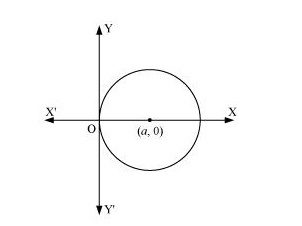
Form the differential equation of the family of circles touching the y-axis at the origin.
The centre of the circle touching the y-axis at origin lies on the x-axis.
Let (a, 0) be the centre of the circle.
Since it touches the y-axis at origin, its radius is a.
Now, the equation of the circle with centre (a, 0) and radius (a) is
$(x-a)^{2}+y^{2}=a^{2}$
$\Rightarrow x^{2}+y^{2}=2 a x$ ...(1)
Differentiating equation (1) with respect to x, we get:
$2 x+2 y y^{\prime}=2 a$
$\Rightarrow x+y y^{\prime}=a$
Now, on substituting the value of a in equation (1), we get:
$x^{2}+y^{2}=2\left(x+y y^{\prime}\right) x$
$\Rightarrow x^{2}+y^{2}=2 x^{2}+2 x y y^{\prime}$
$\Rightarrow 2 x y y^{\prime}+x^{2}=y^{2}$\
This is the required differential equation.
