Show that

(i) $\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}=1$

Left hand side (LHS) = Right hand side (RHS)

Considering LHS,

$=\frac{1}{1+\frac{x^{a}}{x^{b}}}+\frac{1}{1+\frac{x^{b}}{x^{a}}}$

$=\frac{\mathrm{x}^{\mathrm{b}}}{\mathrm{x}^{\mathrm{b}}+\mathrm{x}^{\mathrm{a}}}+\frac{\mathrm{x}^{\mathrm{a}}}{\mathrm{x}^{\mathrm{a}}+\mathrm{x}^{\mathrm{b}}}$

$=\frac{x^{b}+x^{a}}{x^{a}+x^{b}}$

$=1$

Therefore, LHS = RHS

Hence proved

(ii) $\frac{1}{1+x^{b-a}+x^{c-a}}+\frac{1}{1+x^{a-b}+x^{c-b}}+\frac{1}{1+x^{b-c}+x^{a-c}}$

Left hand side (LHS) = Right hand side (RHS)

Considering LHS,

$=\frac{1}{1+\frac{x^{b}}{x^{a}}+\frac{x^{c}}{x^{a}}}+\frac{1}{1+\frac{x^{a}}{x^{b}}+\frac{x^{c}}{x^{b}}}+\frac{1}{1+\frac{x^{b}}{x^{c}}+\frac{x^{a}}{x^{c}}}$

$=\frac{x^{a}}{x^{a}+x^{b}+x^{c}}+\frac{x^{b}}{x^{b}+x^{a}+x^{c}}+\frac{x^{c}}{x^{c}+x^{b}+x^{a}}$

$=\frac{x^{a}+x^{b}+x^{c}}{x^{a}+x^{b}+x^{c}}$

$=1$

Therefore, LHS = RHS

Hence proved

(iii) $\left(x^{\frac{1}{a-b}}\right)^{\frac{1}{a-c}}\left(x^{\frac{1}{b-c}}\right)^{\frac{1}{b-a}}\left(x^{\frac{1}{c-a}}\right)^{\frac{1}{c-b}}$

$=\left(x \frac{1}{(a-b)(a-c)}\right)\left(x \frac{1}{(b-c)(b-a)}\right)\left(x \frac{1}{(c-a)(c-b)}\right)$

$=x \frac{1}{(a-b)(a-c)}+\frac{1}{(b-c)(b-a)}+\frac{1}{(c-a)(c-b)}$

$=x \frac{1}{(a-b)(a-c)}+\frac{-1}{(b-c)(a-b)}+\frac{1}{(a-c)(b-c)}$

$=x \frac{(b-c)}{(a-b)(a-c)(b-c)}+\frac{-(a-c)}{(b-c)(a-b)(a-c)}+\frac{(a-b)}{(a-c)(b-c)(a-b)}$

$=x \frac{b-c-a+c+a-b}{(a-b)(a-c)(b-c)}$

$=x \frac{0}{(a-b)(a-c)(b-c)}$

$=x^{0}=1$

(iv) $\left(\frac{x^{a^{2}}+b^{2}}{x^{a b}}\right)^{a+b}\left(\frac{x^{b^{2}}+c^{2}}{x^{b c}}\right)^{b+c}\left(\frac{x^{c^{2}}+a^{2}}{x^{a c}}\right)^{a+c}=2\left(a^{3}+b^{3}+c^{3}\right)$

$\left(\frac{x^{a^{2}}+b^{2}}{x^{a b}}\right)^{a+b}\left(\frac{x^{b^{2}}+c^{2}}{x^{b c}}\right)^{b+c}\left(\frac{x^{c^{2}}+a^{2}}{x^{a c}}\right)^{a+c}$

$=\left(x^{a^{2}+b^{2}-a b}\right)^{a+b}\left(x^{b^{2}+c^{2}-b c}\right)^{b+c}\left(x^{c^{2}+a^{2}-a c}\right)^{a+c}$

$=\left(\mathrm{x}^{\mathrm{a}+\mathrm{b}\left(\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{ab}\right)}\right)\left(\mathrm{x}^{\mathrm{b}+\mathrm{c}\left(\mathrm{b}^{2}+\mathrm{c}^{2}-\mathrm{bc}\right)}\right)\left(\mathrm{x}^{\mathrm{a}+\mathrm{c}\left(\mathrm{c}^{2}+\mathrm{a}^{2}-\mathrm{ac}\right)}\right)$

$=\left(x^{a^{3}+a b^{2}-a^{2} b+a b^{2}+b^{3}-a b^{2}}\right)\left(x^{b^{3}+b c^{2}-b^{2} c+c b^{2}+c^{3}-b c^{2}}\right)\left(x^{a c^{2}+a^{3}-a^{2} c+c^{3}+a^{2} c-a c^{2}}\right)$

$=\left(x^{a^{3}+b^{3}}\right)\left(x^{b^{3}+c^{3}}\right)\left(x^{a^{3}+c^{3}}\right)$

$=\left(x^{a^{3}+b^{3}+b^{3}+c^{3}+a^{3}+c^{3}}\right)$

$=\left(\mathrm{x}^{2 \mathrm{a}^{3}+2 \mathrm{~b}^{3}+2 \mathrm{c}^{3}}\right)$

$=\left(x^{2\left(a^{3}+b^{3}+c^{3}\right)}\right)$

(vi) $\left[\left(x^{a-a-1}\right)^{\frac{1}{a-1}}\right]^{\frac{a}{a+1}}=x$

$\left[\left(x^{a-a^{-1}}\right)^{\frac{1}{a-1}}\right]^{\frac{a}{a+1}}$

$=\left[\left(x \frac{a-a^{-1}}{a-1}\right)\right]^{\frac{a}{a+1}}$

$=\left[\left(x \frac{a-a^{-1}}{a-1}\right)\right]^{\frac{a}{a+1}}$

$=\left(x \frac{a^{2}-a^{-1+1}}{a^{2}-1}\right)$

$=\left(x \frac{a^{2}-a^{0}}{a^{2}-1}\right)$

$=\left(x \frac{a^{2}-1}{a^{2}-1}\right)$

$=\mathrm{x}^{1}=\mathrm{x}$

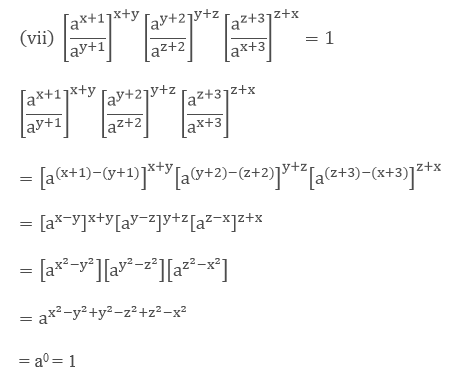
(viii) $\left(\frac{3^{a}}{3^{b}}\right)^{a+b}\left(\frac{3^{b}}{3^{c}}\right)^{b+c}\left(\frac{3^{c}}{3^{a}}\right)^{c+a}=$

$\left(\frac{3^{a}}{3^{b}}\right)^{a+b}\left(\frac{3^{b}}{3^{c}}\right)^{b+c}\left(\frac{3^{c}}{3^{a}}\right)^{c+a}$

$=\left(3^{a-b}\right)^{a+b}\left(3^{b-c}\right)^{b+c}\left(3^{c-a}\right)^{c+a}$

$=3^{a^{2}-b^{2}} \times 3^{b^{2}-c^{2}} \times 3^{c^{2}-a^{2}}$

$=3^{a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2}}$

$=3^{0}=1$