Show that:
(i) (3x + 7)2 − 84x = (3x − 7)2
(ii) (9a − 5b)2 + 180ab = (9a + 5b)2
(iii) $\left(\frac{4 m}{3}-\frac{3 n}{4}\right)^{2}+2 m n=\frac{16 m^{2}}{9}+\frac{9 n^{2}}{16}$
(iv) (4pq + 3q)2 − (4pq − 3q)2 = 48pq2
(v) (a − b)(a + b) + (b − c)(b + c) + (c − a)( c + a) = 0
(i) $\mathrm{LHS}=(3 x+7)^{2}-84 x$
$=(3 x+7)^{2}-4 \times 3 x \times 7$
$=(3 x-7)^{2} \quad\left[\because(a+b)^{2}-4 a b=(a-b)^{2}\right]$
$=$ RHS
Because LHS is equal to RHS, the given equation is verified.
(ii) LHS $=(9 a-5 b)^{2}+180 a b$
$=(9 a-5 b)^{2}+4 \times 9 a \times 5 b$
$=(9 a+5 b)^{2} \quad\left[\because(a-b)^{2}+4 a b=(a+b)^{2}\right]$
= RHS
Because LHS is equal to RHS, the given equation is verified.
(iii) LHS $=\left(\frac{4 m}{3}-\frac{3 n}{4}\right)^{2}+2 m n$
$=\left(\frac{4 m}{3}-\frac{3 n}{4}\right)^{2}+2 \times \frac{4 m}{3} \times \frac{3 n}{4}$
$=\left(\frac{4 m}{3}\right)^{2}+\left(\frac{3 n}{4}\right)^{2} \quad\left[\because(a-b)^{2}+2 a b=a^{2}+b^{2}\right]$
$=\frac{16 m^{2}}{9}+\frac{9 n^{2}}{16}$
$=\mathrm{RHS}$
Because LHS is equal to RHS, the given equation is verified.
(iv) LHS
=(4 p q+3 q)^{2}-(4 p q-3 q)^{2}
$=4(4 p q)(3 q) \quad\left[\because(a+b)^{2}-(a+b)^{2}=4 a b\right]$
$=48 p q^{2}$
$=\mathrm{RHS}$
Because LHS is equal to RHS, the given equation is verified.
(v) LHS $=(a-b)(a+b)+(b-c)(b+c)+(c+a)(c-a)$
$=a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2} \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$
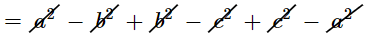
= 0
= RHS
Because LHS is equal to RHS, the given equation is verified.
