Solution:
We know that, $\sqrt{4}=2$
And, $\sqrt{5}=\sqrt{(2)^{2}+(1)^{2}}$
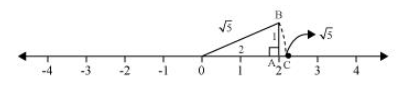
Mark a point ‘A’ representing 2 on number line. Now, construct AB of unit length perpendicular to OA. Then, taking O as centre and OB as radius, draw an arc intersecting number line at C.
$C$ is representing $\sqrt{5}$.
We know that, $\sqrt{4}=2$
And, $\sqrt{5}=\sqrt{(2)^{2}+(1)^{2}}$

Mark a point ‘A’ representing 2 on number line. Now, construct AB of unit length perpendicular to OA. Then, taking O as centre and OB as radius, draw an arc intersecting number line at C.
$C$ is representing $\sqrt{5}$.
