Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution) :

Solution:

The given equations are

$3 x-5 y=20$ $(i)$

$6 x-10 y=-4$$\ldots \ldots .(i i)$

Putting $x=0$ in equation $(i)$, we get:

$\Rightarrow 3 \times 0-5 y=20$

 

$\Rightarrow y=-4$

$x=0, \quad y=-4$

Putting $y=0$ in equation $(i)$ we get

$\Rightarrow 3 x-5 \times 0=20$

$\Rightarrow x=20 / 3$

$x=20 / 3, \quad y=0$

Use the following table to draw the graph.

Draw the graph by plotting the two points $A(0,-4), B(20 / 3,0)$ from table.

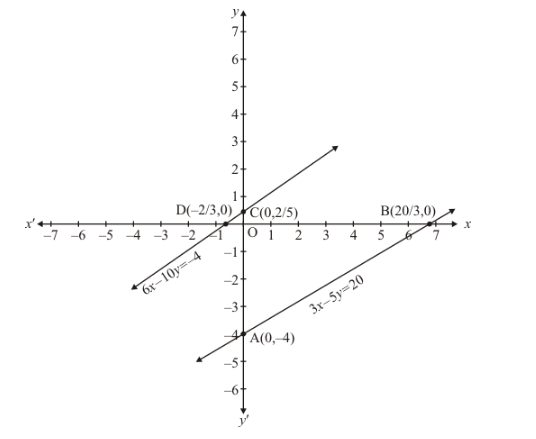
Graph of the equation….

$6 x-10 y=-4$ (ii)

Putting $x=0$ in equation $(i i)$ we get:

$\Rightarrow 6 \times 0-10 y=-4$

$\Rightarrow y=2 / 5$

$x=2 / 5, \quad y=0$

Putting $y=0$ in equation $(i i)$, we get:

$\Rightarrow 6 x-10 \times 0=-4$

$\Rightarrow x=-2 / 3$

$x=-2 / 3, \quad y=0$

Use the following table to draw the graph.

Draw the graph by plotting the two points $C(0,-4), D(20 / 3,0)$ from table.

Here we see that the two lines are parallel 

Hence the given system of equations has no solution.