Question:
S is any point on side QR of a ΔPQR. Show that PQ + QR + RP > 2 PS.
Thinking Process
Use the inequality of a triangle i.e., sum of two sides of a triangle is greater than the third side. Further, show the required result.
Solution:
Given In $\triangle P Q R, S$ is any point on side $Q R$.
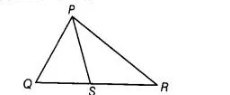
To show $P Q+Q R+R P>2 P S$
Proof $\ln \triangle P Q S$, ... (i)
[sum of two sides of a triangle is greater than the third side]
Similarly, in $\triangle P R S$, $S R+R P>P S$.....(ii)
[sum of two sides of a triangle is greater than the third side]
On adding Eqs. (1) and (ii), we get
$P Q+Q S+S R+R P>2 P S$
$\Rightarrow \quad P Q+(Q S+S R)+R P>2 P S$
$\Rightarrow \quad P Q+Q R+R P>2 P S \quad[\because Q R=Q S+S R]$
