Represent geometrically the following numbers on the number line
(i) $\sqrt{4} .5$
(ii) $\sqrt{5} .6$
(iii) $\sqrt{8.1}$
(iv) $\sqrt{2} .3$
Thinking Process
(i) Firstly, we draw a line segment $A B$ of length equal to the number inside the root and extend it to $C$ such that $B C=1$
(ii) Draw a semi-circle with centre $O$ ( $O$ is the mid-point of $A C$ ) and radius $O A$
(iii) Now, draw a perpendicular line from $B$ to cut the semi-circle atD.
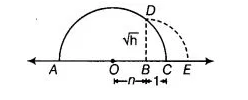
(iv) Further, draw an arc with centre $B$ and radius $B D$ meeting $A C$ produced at $£$
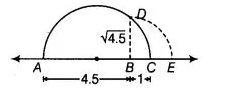
(i) Firstly, we draw a line segment AB = 4.5 units and extend it to C such that BC = 1 unit. Let O be the mid-point of AC.
Now, draw a semi-circle with centre O and radius OA Let us draw BD perpendicular to AC passing through point B and intersecting the semi-circle at point D.
Hence, the distance BD is √4.5 units.
Draw an arc with centre B and radius BD, meeting AC produced at E, then BE = BD = √4.5 units.
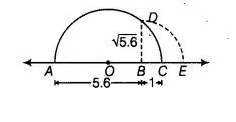
(ii) Firstly, we draw a line segment AB = 5.6 units and extend it to C such that BC = 1 unit. Let O be the mid-point of AC.
Now, draw a semi-circte with centre O and radius OA. Let us draw BD perpendicular to AC passing through point B and intersecting the semi-circle at point D.
Hence, the distance BD is √5.6 units.
Draw an arc with centre B and radius BD, meeting AC produced at E, then BE = BD = √5.6 units.
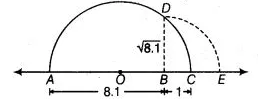
(iii) Firstly, we draw a line segment AB = 8.1 units and extend it toC such that SC = 1 unit. Let O be the mid-point of AC.
Now, draw a semi-circle with centre 0 and radius OA
Let us draw BD perpendicular to AC passing through point 6 intersecting the semi-circle at point D:
Hence, the distance BD is √8.1 units .
Draw an arc with centre Sand radius BD, meeting AC produced at E, then BE = BD = √8.1 units.
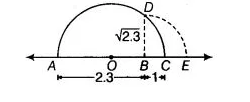
(iv) Firstly, we draw a line segment AS = 2.3 units and extend it to C such that SC = 1 unit. Let O be the mid-point of AC.
Now, draw a semi-circle with centre 0 and radius OA.
Let us draw BD perpendicular to AC passing through point 6 and intersecting the semi-circle at point D.
Hence, the distance BD is √2.3 units.
Draw an arc with centre 6 and radius BD, meeting AC produced at E, then BE = BD = √2.3 units.