Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same).
Volume of the cylindrical part
$=\pi \times(1.5)^{2} \times 8 \mathrm{~cm}^{3}=18 \pi \mathrm{cm}^{3}$
Volume of each conical part
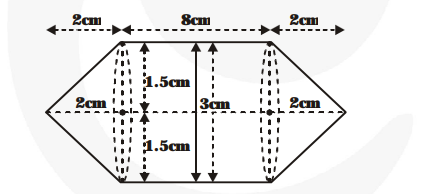
$=\frac{\mathbf{1}}{\mathbf{3}} \pi \times(1.5)^{2} \times 2 \mathrm{~cm}^{3}=\frac{\mathbf{3}}{\mathbf{2}} \pi \mathrm{cm}^{3}$
Therefore, the volume of the air = The volume of cylindrical part + The volumes of two conical parts
$=18 \pi+2 \times \frac{\mathbf{3}}{\mathbf{2}} \pi \mathrm{cm}^{3}=21 \pi \mathrm{cm}^{3}$
$=21 \times \frac{\text { 22 }}{\text { 7 }} \mathrm{cm}^{3}=66 \mathrm{~cm}^{3}$
