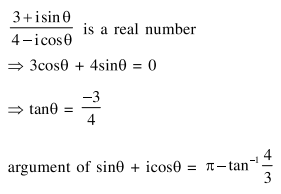Question: If $\frac{3+i \sin \theta}{4-i \cos \theta}, \theta \in[0,2 \pi]$, is a real number, then
an argument of $\sin \theta+i \cos \theta$ is :
$-\tan ^{-1}\left(\frac{3}{4}\right)$
$\tan ^{-1}\left(\frac{4}{3}\right)$
$\pi-\tan ^{-1}\left(\frac{4}{3}\right)$
$\pi-\tan ^{-1}\left(\frac{3}{4}\right)$
Correct Option: , 3
Solution: