Prove the following

(i) Here, $5=2^{2}+1^{2}$

So, draw a right angled $\triangle O A B$, in which $O A=2$ units and $A B=1$ unit and $\angle O A B=90^{\circ}$ By using Pythagoras theorem, we get

$O B=\sqrt{O A^{2}+A B^{2}}$

$=\sqrt{2^{2}+1^{2}}=\sqrt{4+1}=\sqrt{5}$

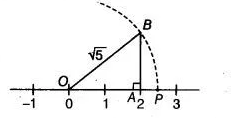
Taking $O B=\sqrt{5}$ as radius and point $O$ as centre, draw an arc which meets the number line at point $P$ on the positive side of it.

Hence, it is clear that point $P$ represents $\sqrt{5}$ on the number line.

(ii) Here, $10=3^{2}+1$

So, draw a right angled $\triangle O A B$, in which $O A=3$ units and $A B=1$ unit and $\angle O A B=90^{\circ}$.

By using Pythagoras theorem, we get

$O B=\sqrt{O A^{2}+A B^{2}}$

$=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10}$

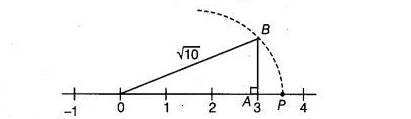
Taking $O B=\sqrt{10}$ as radius and point $O$ as centre, draw an arc which meets the number line at point $P$ on the positive side of it. The point $P$ represents $\sqrt{10}$ on the number line.

(iii) Here, $17=4^{2}+1$

So, draw a right angled $\triangle O A B$, in which $O A=4$ units and $A B=1$ unit and $\angle O A B=90^{\circ}$ By using Pythagoras theorem, we get

$O B=\sqrt{O A^{2}+A B^{2}}$

$=\sqrt{4^{2}+1^{2}}=\sqrt{16+1}=\sqrt{17}$

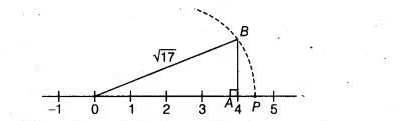
Taking, $O B=\sqrt{17}$ as radius and point $O$ as centre, draw an arc which meets the number line at point $P$ on the positive side of it. The point $P$ represents $\sqrt{17}$ on the number line.