Let $x_{0}$ be the point of local maxima of $f(x)=\vec{a} \cdot(\vec{b} \times \vec{c})$, where
$\vec{a}=x \hat{i}-2 \hat{j}+3 \hat{k}, \quad \vec{b}=-2 \hat{i}+x \hat{j}-\hat{k}$ and $\vec{c}=7 \hat{i}-2 \hat{j}+x \hat{k}$.
Then the value of $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ at $x=x_{0}$ is :
Correct Option: , 4
It is given that
$f(x)=\bar{a} \cdot(\bar{b} \times \bar{c})=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ x & -2 & 3 \\ -2 & x & -1 \\ 7 & -2 & x\end{array}\right|=x^{3}-27 x+26$
$\Rightarrow f(x)=x^{3}-27 x+26$
$\Rightarrow f^{\prime}(x)=3 x^{2}-27$
For critical point $f^{\prime}(x)=0$
$\Rightarrow 3 x^{2}-27=0 \Rightarrow x=-3,3$
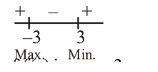
The local maxima of $f(x)$ is, $x_{0}=-3$.
Then $\bar{a} \cdot \bar{b}+\bar{b} \cdot \bar{c}+\bar{c} \cdot \bar{a}$
$=-2 x-2 x-3-14-2 x-x+7 x+4+3 x=3 x-13$
So, value at $x=x_{0},=\bar{a} \cdot \bar{b}+\bar{b} \cdot \bar{c}+\bar{c} \cdot \bar{a}=3 x-13$
$=3 \times(-3)-13=-22$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.