Question:
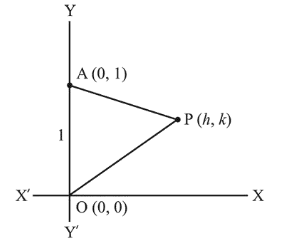
Let $\mathrm{O}(0,0)$ and $\mathrm{A}(0,1)$ be two fixed points. Then the locus of a point $\mathrm{P}$ such that the perimeter of $\triangle \mathrm{AOP}$ is 4 , is :
Correct Option: , 3
Solution:
Let point $P(h, k)$
$O A=1$
So, $O P+A P=3$
$\Rightarrow \sqrt{h^{2}+k^{2}}+\sqrt{h^{2}+(k-1)^{2}}=3$
$\Rightarrow h^{2}+(k-1)^{2}=9+h^{2}+k^{2}-6 \sqrt{h^{2}+k^{2}}$
$\Rightarrow 6 \sqrt{h^{2}+k^{2}}=2 k+8$
$\Rightarrow 9 h^{2}+8 k^{2}-8 k-16=0$
Hence, locus of point $\mathrm{P}$ is
$9 x^{2}+8 y^{2}-8 y-16=0$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.