$\int \frac{x^{\frac{1}{2}}}{1+x^{\frac{3}{4}}} d x$ (hint : Put $\left.x=z^{4}\right)$
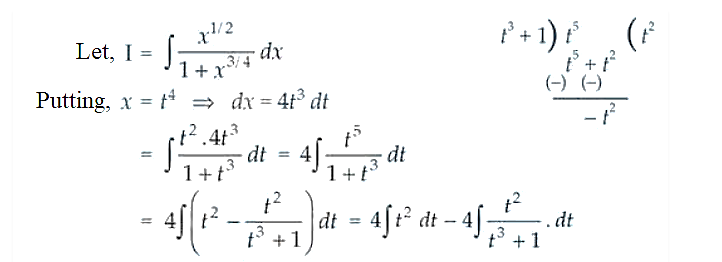
Let's consider, $I=I_{1}-I_{2}$
Now, $\mathrm{I}_{1}=4 \int t^{2} d t=4 \cdot \frac{t^{3}}{3}+C_{1}=\frac{4}{3} x^{3 / 4}+C_{1}$
$I_{2}=4 \int \frac{t^{2}}{t^{3}+1} d t$
Putting, $t^{3}+1=z \Rightarrow 3 t^{2} d t=d z$
$t^{2} d t=\frac{1}{3} d z$
So, $\quad I_{2}=\frac{4}{3} \int \frac{d z}{z}=\frac{4}{3} \log |z|+C_{2}=\frac{4}{3} \log \left|t^{3}+1\right|+C_{2}$
$=\frac{4}{3} \log \left|(x)^{3 / 4}+1\right|+C_{2}$
As, $\quad \mathrm{I}=\mathrm{I}_{1}-\mathrm{l}_{2}$
$=\frac{4}{3} x^{3 / 4}+C_{1}-\frac{4}{3} \log \left|(x)^{3 / 4}+1\right|-C_{2}$
$=\frac{4}{3}\left[x^{3 / 4}-\log \left|(x)^{3 / 4}+1\right|\right]+C_{1}-C_{2}$
Therefore, $\mathrm{I}=\frac{4}{3}\left[x^{3 / 4}-\log \left|(x)^{3 / 4}+1\right|\right]+C \quad\left[\because \mathrm{C}=\mathrm{C}_{1}-\mathrm{C}_{2}\right.$
