Prove that through a given point,

Given Consider a line l and a point P.

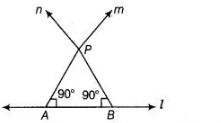
Construction Draw two intersecting lines passing through the point $P$ and which is perpendicular to $l$.

To prove Only one perpendicular line can be drawn through a given point i.e., to prove

$\angle P=0^{\circ}$

Proof In $\triangle A P B, \quad \angle A+\angle P+\angle B=180^{\circ}$

[by angle sum property of a triangle is $180^{\circ}$ ]

$\Rightarrow$ $90^{\circ}+\angle P+90^{\circ}=180^{\circ}$

$\Rightarrow$ $\angle P=180^{\circ}-180^{\circ}$

$\therefore$ $\angle P=0^{\circ}$

So, lines $n$ and $m$ coincide.

Hence, only one perpendicular line can be drawn through a given point.