Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

In the figure, PQ is diameter of the given circle and O is its centre.

Let tangents AB and CD be drawn at the end points of the diameter PQ.

Since, the tangents at a point to a circle is perpendicular to the radius through the point. 

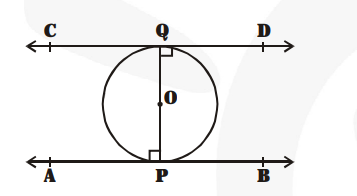
$\therefore \quad \mathrm{PQ} \perp \mathrm{AB}$

$\Rightarrow \mathrm{APQ}=90^{\circ}$ and $\mathrm{PQ} \perp \mathrm{CD}$

$\Rightarrow \quad \angle \mathrm{PQD}=90^{\circ}$

$\Rightarrow \angle \mathrm{APQ}=\angle \mathrm{PQD}$b

But they form a pair of alternate angles.

$\therefore \mathrm{AB} \| \mathrm{CD}$

Hence, the two tangents are parallel.