Prove that the tangents drawn at the ends

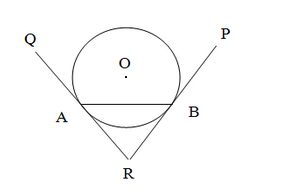
Let $R A$ and $R B$ be two tangents to the circle with centre $O$ and let $A B$ be $a$ chord of the circle.

We have to prove that $\angle R A B=\angle R B A$.

$\therefore$ Now, $R A=R B$ (Since tangents drawn from an external point to a circle are equal)

$\therefore$ In $\Delta R A B, \angle R A B=\angle R B A$ (S ince opposite sides are equal, their base angles are also equal)