Prove that the ratio of the areas of two similar triangles is equal

Solution:

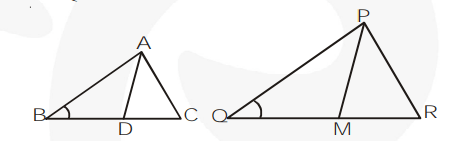
In figure, $\mathrm{AD}$ is a median of $\triangle \mathrm{ABC}$ and $\mathrm{PM}$ is a median of $\triangle \mathrm{PQR}$. Here, $\mathrm{D}$ is mid-point of $\mathrm{BC}$ and $M$ is mid-point of $Q R$.

Now, we have $\triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$.



$\Rightarrow \angle \mathrm{B}=\angle \mathrm{Q}$ ...(1)

(Corresponding angles are equal)

Also $\quad \frac{A B}{P Q}=\frac{B C}{Q R}$

(Ratio of corresponding sides are equal)

$\Rightarrow \frac{A B}{P Q}=\frac{2 B D}{2 Q M}$

( $\because \mathrm{D}$ is mid-point of $\mathrm{BC}$ and $\mathrm{M}$ is mid-point of $\mathrm{QR}$ )

$\Rightarrow \frac{A B}{P O}=\frac{B D}{Q M}$ ...(2)

In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{POM}$

$\angle \mathrm{ABD}=\angle \mathrm{PQM}$ (by1)

and $\frac{A B}{P Q}=\frac{B D}{O M}$(by2)

$\Rightarrow \Delta \mathrm{ABD} \sim \Delta \mathrm{PQM}$ (SAS similarity) $\Rightarrow \frac{A B}{P Q}=\frac{A D}{P M}$ ...(3)

Now, $\frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\frac{A B^{2}}{P Q^{2}}$ (SAS similarity)

$\Rightarrow \frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P O R)}=\frac{A D^{2}}{P M^{2}} \quad\left(\because \frac{A B}{P Q}=\frac{A D}{P M}\right)$