Prove that the points A

If two lines having the same slope pass through a common point, then two lines will coincide. Hence, if A, B and C are three points in the XY - plane, then they will lie on a line, i.e., three points are collinear if and only if slope of AB = slope of BC.

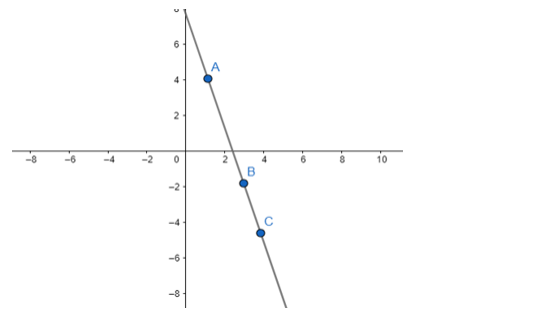
Slope of AB = slope of BC

$\frac{-2-4}{3-1}=\frac{-5-(-2)}{4-3} \Rightarrow \frac{-6}{2}=\frac{-3}{1}$

$-3=-3$

Hence verified, i.e. points are collinear. Now using two point form of the equation

$\mathrm{y}-\mathrm{y}_{1}=\frac{\mathrm{y}_{2}-\mathrm{y}_{1}}{\mathrm{x}_{2}-\mathrm{x}_{1}}\left(\mathrm{x}-\mathrm{x}_{1}\right)$ where $\frac{\mathrm{y}_{2}-\mathrm{y}_{1}}{\mathrm{x}_{2}-\mathrm{x}_{1}}=$ slope of line

$y-4=-3(x-1)$

$y-4+3 x-3=0$

$3 x+y-7=0$

So, required equation of line is 3x + y - 7.