Prove that the perpendicular at the point of contact to

Let us first put the given data in the form of a diagram. Let us also draw another parallel tangent PQ parallel to the given tangent AB. Draw a radius OR to the point of contact of the tangent PQ. Let us also draw a radius CO parallel to the two tangents.

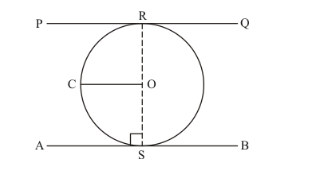
It is given that,

We know that sum of angles on the same side of the transversal will be equal to 180°. Therefore,

$\angle O S A+\angle C O S=180^{\circ}$

$90^{\circ}+\angle C O S=180^{\circ}$

$\angle C O S=90^{\circ}$   ..........(1)

We know that the radius of the circle will always be perpendicular to the tangent at the point of contact. Therefore,

Again, since sum of angles on the same side of the transversal is equal to 180°, we have,

$\angle P R O+\angle C O P=180^{\circ}$

$90^{\circ}+\angle C O P=180^{\circ}$

$\angle C O P=90^{\circ}$...........(2)

Now let us add equation (1) and (2). We get,

$\angle C O S+\angle C O P=90^{\circ}+90^{\circ}$

$\angle C O S+\angle C O P=180^{\circ}$

Looking at the figure we can rewrite the above equation as,

We know that the angle of a straight line will measure 180°. Therefore, ROS is the straight line. Also, RO is the radius which we have drawn and we know that a radius is always drawn from the centre of the circle. Therefore, line ROS passes through the centre of the circle.

Thus we have proved that the perpendicular to the tangent at the point of contact passes through the centre of the circle.