Prove that the parallelogram circumscribing a circle is a rhombus.

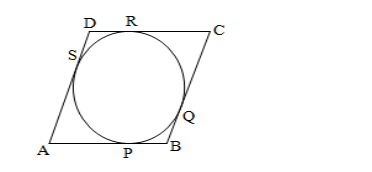
Given, a parallelogram ABCD circumscribes a circle with centre O.

$A B=B C=C D=A D$

We know that the lengths of tangents drawn from an exterior point to a circle are equal.

$\therefore A P=A S \ldots \ldots(i) \quad[$ tangents from $A]$

$B P=B Q \ldots . \ldots \ldots(i i) \quad[$ tangents from $B]$

$C R=C Q \ldots \ldots \ldots(i i i) \quad[$ tangents from $C]$

$D R=D S \ldots \ldots \ldots \ldots(i v) \quad[$ tangents from $D]$

$\therefore A B+C D=A P+B P+C R+D R$

$=A S+B Q+C Q+D S[$ from $(i),(i i),(i i i)$ and $(i v)]$

$=(A S+D S)+(B Q+C Q)$

$=A D+B C$

Thus, $(A B+C D)=(A D+B C)$

$\Rightarrow 2 A B=2 A D \quad[\because$ opposite sides of a parallelogram are equal $]$

$\Rightarrow A B=A D$

$\therefore C D=A B=A D=B C$

Hence, ABCD is a rhombus.