Question:
Prove that the line segments joining the middle points of the sides of a triangle divide it into four congruent triangles.
Solution:
∆ABC is shown below. D, E and F are the midpoints of sides AB, BC and CA, respectively.
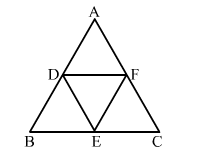
As, D and E are the mid points of sides AB, and BC of ∆ ABC.
∴ DE ∣∣ AC (By midpoint theorem)
Similarly, DF ∣∣ BC and EF ∣∣ AB.
Therefore, ADEF, BDFE and DFCE are all parallelograms.
Now, DE is the diagonal of the parallelogram BDFE.
∴ ∆BDE ≅ ∆FED
Simiilarly, DF is the diagonal of the parallelogram ADEF.
∴ ∆DAF ≅ ∆FED
And, EF is the diagonal of the parallelogram DFCE.
And, EF is the diagonal of the parallelogram DFCE.
∴ ∆EFC ≅ ∆FED
So, all the four triangles are congruent.
So, all the four triangles are congruent.
