Prove that the length of two tangents drawn from an external point to a circle are equal.

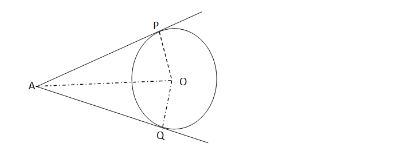
Given two tangents AP and AQ are drawn from a point A to a circle with centre O.

To prove: $A P=A Q$

Join $O P, O Q$ and $O A$.

$A P$ is tangent at $P$ and $O P$ is the radius.

$\therefore O P \perp A P($ since tangents drawn from an external point are

perpendicular to the radius at the point of contact)

Similarly, $O Q \perp A Q$

In the right $\triangle O P A$ and $\triangle O Q A$, we have:

$O P=O Q \quad$ [radii of the same circle]

$\angle O P A=\angle O Q A\left(=90^{\circ}\right)$

$O A=O A \quad[$ common side $]$

$\therefore \Delta O P A \cong \Delta O Q A \quad[$ By R. H. S - Congruence $]$

Hence, $A P=A Q$