Prove that the least perimeter of an isosceles triangle i

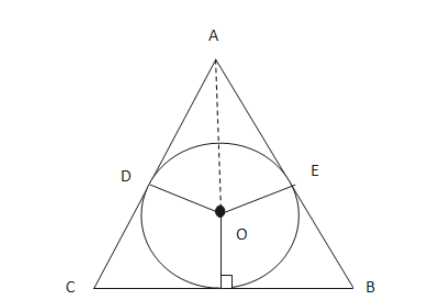
Let $\mathrm{ABC}$ is an isosceles triangle with $\mathrm{AB}=\mathrm{AC}=x$ and a circle with centre $\mathrm{O}$ and radius $r$ is inscribed in the triangle.

$\mathrm{O}, \mathrm{A}$ and $\mathrm{O}, \mathrm{E}$ and $\mathrm{O}, \mathrm{D}$ are joined.

From $\Delta \mathrm{ABF}$

$\mathrm{AF}^{2}+\mathrm{BF}^{2}=\mathrm{AB}^{2}$

$\Rightarrow(3 r)^{2}+\left(\frac{y}{2}\right)^{2}=x^{2} \quad \ldots(1)$

Again,From $\Delta \mathrm{ADO},(2 r)^{2}=r^{2}+\mathrm{AD}^{2}$

$\Rightarrow 3 r^{2}=\mathrm{AD}^{2}$

$\Rightarrow \mathrm{AD}=\sqrt{3} r$

Now, $\mathrm{BD}=\mathrm{BF}$ and $\mathrm{EC}=\mathrm{FC}$ (Since tangents drawn from an external point are equal)

Now, $\mathrm{AD}+\mathrm{DB}=x$

$\Rightarrow(\sqrt{3} r)+\left(\frac{y}{2}\right)=x$

$\Rightarrow \frac{y}{2}=x-\sqrt{3} \quad \ldots(2)$

$\therefore(3 r)^{2}+(x-\sqrt{3} r)^{2}=x^{2}$

$\Rightarrow 9 r^{2}+x^{2}-2 \sqrt{3} r x+3 r^{2}=x^{2}$

$\Rightarrow 12 r^{2}=2 \sqrt{3} r x$

$\Rightarrow 6 r=\sqrt{3} x$

$\Rightarrow x=\frac{6 r}{\sqrt{3}}$

Now, From (2),

$\frac{y}{2}=\frac{6}{\sqrt{3}} r-\sqrt{3} r$

$\Rightarrow \frac{y}{2}=\frac{6 \sqrt{3}}{3} r-\sqrt{3} r$

$\Rightarrow \frac{y}{2}=\frac{(6 \sqrt{3}-3 \sqrt{3}) r}{3}$

$\Rightarrow \frac{y}{2}=\frac{3 \sqrt{3} r}{3}$

$\Rightarrow y=2 \sqrt{3} r$

Perimeter $=2 x+y$

$=2\left(\frac{6}{\sqrt{3}} r\right)+2 \sqrt{3} r$

$=\frac{12}{\sqrt{3}} r+2 \sqrt{3} r$

$=\frac{12 r+6 r}{\sqrt{3}}$

$=\frac{18}{\sqrt{3}} r$

$=\frac{18 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} r$

$=6 \sqrt{3} r$