Prove that the diameter of a circle perpendicular to one of the two parallel chords of a circle is perpendicular to the other and bisects it.

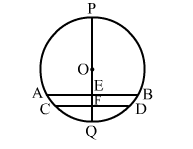
Given: AB and CD are two parallel chords of a circle with centre O.
POQ is a diameter which is perpendicular to AB.
To prove: PF ⊥ CD and CF = FD
Proof:
AB || CD and POQ is a diameter.
∠PEB = 90°    (Given)
∠PFD = ∠PEB          (∵ AB || CD, Corresponding angles)
Thus, PF ⊥ CD 
∴ OF ⊥ CD
We know that the perpendicular from the centre to a chord bisects the chord.
i.e., CF = FD
Hence, POQ is perpendicular to CD and bisects it.