Prove that the centres of the three circles

Given,

$x^{2}+y^{2}-4 x-6 y-12=0$

centre $\left(-g_{1},-f_{1}\right)=(2,3)$

$x^{2}+y^{2}+2 x+4 y-5=0$

centre $\left(-g_{2},-f_{2}\right)=(-1,-2)$

$x^{2}+y^{2}-10 x-16 y+7=0$

centre $\left(-g_{3},-f_{3}\right)=(5,8)$

to prove that the centres are collinear,

$\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3} & 1\end{array}\right|=0$

Where $x_{1}, y_{1}$ are the coordinates of the ist centre and so on.

$\Rightarrow\left|\begin{array}{ccc}2 & 3 & 1 \\ -1 & -2 & 1 \\ 5 & 8 & 1\end{array}\right|$

$=2(-2-8)-3(-1-5)+1(-8+10)$

$=-20+18+2=0$

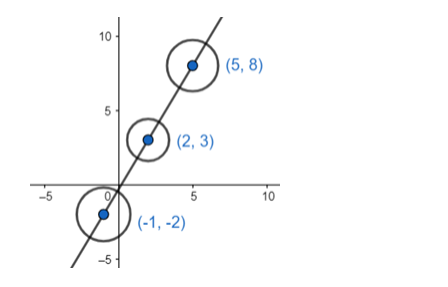
The centres are collinear