Prove that the angles between the two tangents drawn form an external point to a circle is supplementary to the angle subtended

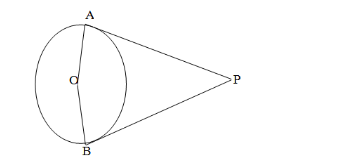
Given, PA and PB are the tangents drawn from a point P to a circle with centre O. Also, the line segments OA and OB are drawn.

To prove : $\angle A P B+\angle A O B=180^{\circ}$

We know that the tangent to a circle is perpendicular to the radius through the point of contact.

$\therefore P A \perp O A$

$\Rightarrow \angle O A P=90^{\circ}$

$P B \perp O B$

$\Rightarrow \angle O B P=90^{\circ}$

$\therefore \angle O A P+\angle O B P=\left(90^{0}+90^{0}\right)=180^{0} \quad \ldots \ldots$ (i)

But we know that the sum of all the angles of a quadrilateral is $360^{\circ}$.

$\therefore \angle O A P+\angle O B P+\angle A P B+\angle A O B=360^{\circ} \quad \ldots \ldots \ldots$. (ii)

From (i) and (ii), we get:

$\angle A P B+\angle A O B=180^{\circ}$