Prove that sum of any two sides of a triangle

Given $\ln \triangle A B C, A D$ is a median.

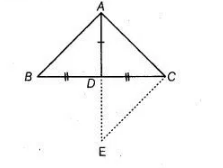
Construction

Produce $A D$ to a point $E$ such that $A D=D E$ and join $C E$.

To prove $A C+A B>2 A D$

Proof In $\triangle A B D$ and $\triangle E C D$,

$A D=D E$ [by construction]

$B D=C D$ [given $A D$ is the median]

and $\angle A D B=\angle C D E$ [vertically opposite angle]

$\therefore$ $\triangle \mathrm{ABD} \equiv \triangle \mathrm{ECD}$ [by SAS congruence rule]

$\Rightarrow$ $A B=C E$ [by CPCT] ...(i)

Now, in $\triangle A E C$,

$A C+E C>A E$   [sum of two sides of a triangle is greater than the third side]

$\therefore \quad A C+A B>2 A D$ [from Eq. (i) and also taken that $A D=D E]$

Hence proved.