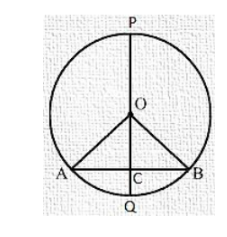
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at
Question:
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution:
Given:
PQ is a diameter of circle which bisects the chord AB at C.
To Prove: PQ bisects ∠AOB
Proof:
In ∠AOC and ∠BOC
OA = OB [Radius of circle]
OC = OC [Common]
AC = BC [Given]
Then ΔAOC ≅ ΔBOC [By SSS condition]
∠AOC = ∠BOC [C.P.C.T]
Hence PQ bisects ∠AOB.