Prove that:

To Prove: $2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31}=\frac{\pi}{4}$

Formula Used:

1) $2 \sin ^{-1} x=\sin ^{-1}\left(2 x x \sqrt{1-x^{2}}\right)$

2) $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x y<1$

Proof:

$\mathrm{LHS}=2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31} \ldots$ (1)

$2 \sin ^{-1} \frac{3}{5}=\sin ^{-1}\left(2 \times \frac{3}{5} \times \sqrt{1-\left(\frac{3}{5}\right)^{2}}\right)$

$=\sin ^{-1}\left(\frac{6}{5} \times \frac{4}{5}\right)$

$=\sin ^{-1} \frac{24}{25} \ldots$ (2)

Substituting $(2)$ in $(1)$, we get

$\mathrm{LHS}=\sin ^{-1} \frac{24}{25}-\tan ^{-1} \frac{17}{31} \ldots$ (3)

Let $\sin \theta=\frac{24}{25}$

Therefore $\theta=\sin ^{-1} \frac{24}{25} \ldots$ (4)

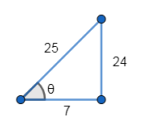
From the figure, $\tan \theta=\frac{24}{7}$

$\Rightarrow \theta=\tan ^{-1} \frac{24}{7} \ldots$ (5)

From (4) and (5),

$\sin ^{-1} \frac{24}{25}=\tan ^{-1} \frac{24}{7} \ldots$ (6)

Substituting (6) in (3), we get

$\mathrm{LHS}=\tan ^{-1} \frac{24}{7}-\tan ^{-1} \frac{17}{31}$

$=\tan ^{-1}\left(\frac{\frac{24}{7}-\frac{17}{31}}{1+\left(\frac{24}{7} \times \frac{17}{31}\right)}\right)$

$=\tan ^{-1}\left(\frac{744-119}{217+408}\right)$

$=\tan ^{-1} \frac{625}{625}$

$=\tan ^{-1} 1$

$=\frac{\pi}{4}$

$=\mathrm{RHS}$

Therefore, LHS = RHS

Hence proved.