Question:
Prove that sin-1 8/17 + sin-1 3/5 = sin-1 77/85
Solution:
Taking the L.H.S,
= sin-1 8/17 + sin-1 3/5
$=\tan ^{-1} \frac{\frac{8}{15}+\frac{3}{4}}{1-\frac{8}{15} \times \frac{3}{4}}$
$=\tan ^{-1} \frac{\frac{32+45}{60}}{\frac{60-24}{60}}$
$=\tan ^{-1} 8 / 15+\tan ^{-1} 3 / 4$
$=\tan ^{-1} \frac{77}{36}$
$=\sin ^{-1} \frac{77}{\sqrt{5929+1296}}$
$=\sin ^{-1} \frac{77}{85}$
$=$ R.H.S.
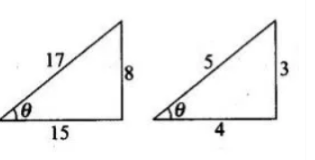
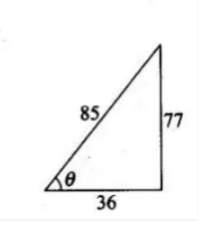
– Hence proved
